===============================================
JOYCE Parameterization starts
===============================================
---------------
A) Scanning input file
---------------
input file ok
Frequency plot required: joyce.but_freqchk.agr
Torsions plot required: but_torschk
Title: | Butane - Step 2 |
---------------
B) Reading QM training data
---------------
QM INPUT FILE for geom-0 (QM): ../../QMdata/opt+freq.fcc
============ reading FCC data ===========
title: Butane opt geom + freq
n.atoms ........................... 14
E(tot) ............................ -158.45877100
In the above frame, the first two sections of the joyce. molname.out log file are reported.
In section 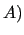 , J OYCE3.0 scans the input file and checks its validity.
Thereafter, prints some info on the required plot files (if any) and on the project title. In the second section, J OYCE prints some information retrieved from the QM database (here in 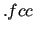 format).
In particular, the QM reference energy ( 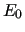 ) appearing in equation ( 35) is recovered and printed ( E(tot)).
From the QM optimized geometry J OYCE3.0 also recovers the connection table of the target
molecule T. It reconstructs the molecular connectivity from the atomic covalent radii implemented in the code and the related bond orders.
Note that this information can be printed in the output by increasing the print level through the print key.
In the same section, as reported in the frame below, J OYCE3.0 recovers, based on the bond orders computed for the optimized geometry,
all intramolecular coordinates
(bonds, angles and dihedrals), called natural IC or NIC, printing their labels (according to the atom
names found in the QM database) and equilibrium values.
====== INTERN COORD analysis: NATURAL-ICs: style=FF ======
TYPE NAME EQUIL.VALUE
Angs or deg
1 distance C1-C2 1.5302 1 2
2 distance C2-C3 1.5325 2 3
[...]
19 angle C1-C2-H9 109.5439 1 2 9
20 angle C2-C3-C4 113.3938 2 3 4
[...]
38 dihedral C1-C2-C3-C4 -179.9998 1 2 3 4
[...]
64 dihedral H11-C3-C4-H14 -178.0147 11 3 4 14
In the last columns, the numbers (which refer to the atom order found in .fcc file) of the atoms involved in the definition of each NIC are also indicated.
All the recovered NIC are printed in the generated.IC.txt
output file (see subsection 6.2).
In the third section, JOYCE3.0's output shows instead the set of ICs defined in the GROMACS topology file, are printed together with their equilibrium value (computed from the QM optimized geometry), as shown in the following.
---------------
C) Reading FF & IC definition
---------------
Gromacs input file ..........: but.step2.top
1) Atom Types
Site Name Charge Mass Sigma Epsilon
1 C1 0.000 12.011 0.350 0.276
2 C2 0.000 12.011 0.350 0.276
3 H1 0.000 1.008 0.250 0.126
4 H2 0.000 1.008 0.250 0.126
2) Stretching parameters
Bond Atoms k_s r0 FF term Atoms
1 C1 C2 2254.51 1.530 1 1 2
2 C2 C2 2130.51 1.533 2 2 3
[...]
13 C1 H1 3100.08 1.104 13 4 14
3) Bending parameters
Angle Atoms k_b theta0 FF term Atoms
1 C1 C2 C2 710.63 113.390 14 1 2 3
2 C2 C1 H1 346.67 111.620 15 2 1 5
[...]
22 H1 C1 H1 313.34 107.580 35 12 4 13
23 H1 C1 H1 313.34 107.580 36 12 4 14
24 H1 C1 H1 313.34 107.330 37 13 4 14
4.2) Fourier torsions
Dihedral Atoms Ncos K_d n gamma FF term Atoms
1 C1 C2 C2 C1 5 0.0000 0 0.00 38 1 2 3 4
0.0000 1 0.00 39
0.0000 2 0.00 40
0.0000 3 0.00 41
0.0000 4 0.00 42
2 H1 C1 C2 C2 1 0.0000 3 0.00 43 5 1 2 3
3 H1 C1 C2 C2 1 0.0000 3 0.00 44 6 1 2 3
4 H1 C1 C2 C2 1 0.0000 3 0.00 45 7 1 2 3
5 C2 C2 C1 H1 1 0.0000 3 0.00 46 2 3 4 12
6 C2 C2 C1 H1 1 0.0000 3 0.00 47 2 3 4 13
7 C2 C2 C1 H1 1 0.0000 3 0.00 48 2 3 4 14
The following functions keep the R0/Ang0/Gamma values as given in FF file
38 C1-C2-C2-C1_n=0
39 C1-C2-C2-C1_n=1
40 C1-C2-C2-C1_n=2
41 C1-C2-C2-C1_n=3
42 C1-C2-C2-C1_n=4
43 H1-C1-C2-C2_n=3
44 H1-C1-C2-C2_n=3
45 H1-C1-C2-C2_n=3
46 H1-C1-C2-C2_n=3
47 H1-C1-C2-C2_n=3
48 H1-C1-C2-C2_n=3
If the $keepff keyword is activated, a list of the selected IC equilibrium values (constrained to the value read from the topology file) is also given at this point, as shown above.
It is important to stress once again that the set of IC defining the FF and effectively employed during the parameterization is the one read from the GROMACS topology file.
This set can be arbitrarily chosen by the user, depending on the characteristics of the target molecule T (as illustrated in section 7.1.2 and Figure 6), and the number of IC that compose it can exceed 3N-6, N being the number of atoms of the molecule.
For these reason,
as mentioned in section 7.1.2, the IC selected in the topology file are named as redundant IC (RIC).
Once the RIC set has been defined the parameterization procedure starts.
First of all, JOYCE3.0 associates a model function to each RIC, as assigned in the topology file.
Thereafter, the program starts retrieving information from the QM training database, concretely by considering T's optimize geometry and Hessian matrix.
From such info, QM vibrational modes and frequency are analyzed in terms of the defined RICS, and the results printed as follows:
---------------
D) Working with the QM Hessian
---------------
INCREMENT Alpha, Beta matrices for ABSOLUTE MINIMUM GEOMETRY
Energy weight ...................... 0.0000
Gradient weights ................... 0.0000
diag Hessian weights ............... 5000.0000
off-diag Hessian weights ........... 2500.0000
further freq dep. weight for Hessian -1.0000
=====================================================
N O R M A L V I B R A T I O N A L M O D E S
GEOMETRY 0
=====================================================
Compute the Mass weighted Hessian
Diagonalize the Mass weighted Hessian
Eigenvalues of the (M-1/2)*F*M(-1/2) matrix (mH)GEOMETRY 0
1 0.3141E-03 2 0.1080E-02 3 0.1377E-02 4 0.1490E-02 5 0.3745E-01
6 0.1143E-01 7 0.1360E-01 8 0.1482E-01 9 0.1895E-01 10 0.1980E-01
11 0.2179E-01 12 0.2396E-01 13 0.2809E-01 14 0.2975E-01 15 0.3388E-01
16 0.3566E-01 17 0.3623E-01 18 0.3996E-01 19 0.4058E-01 20 0.4063E-01
21 0.4425E-01 22 0.4444E-01 23 0.4478E-01 24 0.4489E-01 25 0.4537E-01
26 0.4577E-01 27 0.1871 28 0.1879 29 0.1893 30 0.1895
31 0.1899 32 0.1927 33 0.1978 34 0.1983 35 0.1989
36 0.1990
Frequencies in 1/cm GEOMETRY 0
1 123.003 2 228.124 3 257.531 4 267.883 5 424.756
6 741.881 7 809.383 8 844.930 9 955.322 10 976.484
11 1024.469 12 1074.392 13 1163.236 14 1197.042 15 1277.571
16 1310.553 17 1320.966 18 1387.318 19 1398.026 20 1399.016
21 1459.989 22 1463.041 23 1468.742 24 1470.551 25 1478.275
26 1484.835 27 3002.068 28 3008.730 29 3019.914 30 3021.358
31 3024.177 32 3046.798 33 3087.033 34 3090.517 35 3095.316
36 3096.069
JOYCE recovers the Cartesian Hessian matrix from the QM optimized geometry and computes mass weighted Hessian, normal modes and
frequencies according to equations (27)-(30). Note that translation and rotations are not considered.
As shown in the above frame, it prints all the information gained, numbering the frequencies (and the corresponding
normal modes) from the lowest to the highest.
For each normal mode, JOYCE3.0 computes its projection over the set of selected RIC, printing them in a matrix form, where each column contains the coefficients of the normal mode corresponding to the reported frequency projected over the RIC.
Each row contains up to 10 columns.
In the example framed here below, we show how this simple analysis gives a quick snapshot on how the vibrations distribute themselves over the RIC.
As could be expected, the lowest frequencies involve many RIC, essentially dihedrals, whereas high frequency ones are more localized in stretching or bending RIC.
It is crucial to stress here that such analysis gives hints about which IC should be considered as flexible (and as such represented through periodic functions) or stiff (to be accounted for via harmonic potentials).
VIBRATIONAL NORMAL MODES: Int.Coord. displac.s GEOMETRY 0
123.2 228.4 257.7 267.9 424.7 ...
1 2 3 4 5 ...
1 C1-C2 0.000 0.000 0.003 0.000 -0.021 ...
2 C2-C2 0.000 0.000 0.000 0.000 -0.019 ...
3 C2-C1 0.000 0.000 -0.003 0.000 -0.021 ...
14 C1-C2-C2 0.000 0.000 -0.064 0.000 -0.051 ...
15 C2-C2-C1 0.000 0.000 0.064 0.000 -0.051 ...
16 C2-C1-H 0.000 0.000 0.017 0.000 0.024 ...
[...]
38 C1-C2-C2-C1 -0.207 0.043 0.000 0.000 0.000 ...
39 H-C1-C2-C2 -0.039 -0.177 0.000 -0.197 0.000 ...
40 C2-C2-C1-H -0.039 -0.177 0.000 0.197 0.000 ...
41 C1-C1 0.000 0.000 0.000 0.000 -0.159 ...
42 H-C1 0.169 -0.044 -0.173 0.002 -0.119 ...
43 H-C1 -0.169 0.044 -0.173 -0.002 -0.119 ...
[...]
3024.1 3046.8 3087.0 3090.5 3095.4 3096.1
31 32 33 34 35 36
4 C1-H 0.000 0.000 0.000 0.000 -0.265 -0.279
5 C1-H 0.040 0.088 -0.273 -0.290 0.108 0.118
6 C1-H -0.040 -0.088 0.273 0.290 0.107 0.118
7 C1-H 0.000 0.000 0.000 0.000 -0.263 0.281
8 C1-H -0.040 0.088 0.273 -0.290 0.107 -0.119
9 C1-H 0.040 -0.088 -0.273 0.290 0.107 -0.119
10 C2-H -0.234 -0.238 -0.046 -0.108 -0.015 -0.022
11 C2-H 0.234 0.238 0.046 0.108 -0.015 -0.022
12 C2-H -0.234 0.238 -0.046 0.108 -0.015 0.022
13 C2-H 0.234 -0.238 0.046 -0.108 -0.015 0.022
16 C2-C1-H 0.000 0.000 0.000 0.000 0.013 0.014
17 C2-C1-H -0.010 -0.014 0.013 0.012 -0.007 -0.007
18 C2-C1-H 0.010 0.014 -0.013 -0.012 -0.007 -0.007
19 H-C1-H -0.002 -0.003 0.012 0.014 0.006 0.006
20 H-C1-H 0.002 0.003 -0.012 -0.014 0.006 0.006
End Normal Modes Calculation
Computed Alpha,Beta for HESSIAN points 1 666
Computed 666 new points for geom:
ABSOLUTE MINIMUM GEOMETRY
If flexible ICs are present, and a QM relaxed scan is given to JOYCE in the 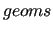 section of the input file, the code starts a loop on all given geometries, printing the results in section section of the input file, the code starts a loop on all given geometries, printing the results in section 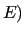 of the output file.
All scanned geometries go through the following operations: of the output file.
All scanned geometries go through the following operations:
- i) Cartesian coordinates and the total energy are read for each geometry from the QM database
- ii) FIRA is applied to the current geometry by performing a rigid rotation of the scanned dihedral, starting from the fully optimized geometries and displacing the chosen dihedral to the value computed from the QM current constrained optimization.
- iii) The QM relaxed energy read from the training database is associated with the new geometry obtained through FIRA.
The following analysis is only performed on geometries other than the absolute minimum,
thus it will only be activated if an energy scan has been performed on some selected RIC.
----------------
E) Working with relaxed QM scans
----------------
========================================
GEOMETRY n. 1
========================================
QM input file: ../../QMdata/Scan1/butane.delta_000.fcc
============ reading FCC data ===========
title: State file generated from file: butane.delta_000.fchk (format: fchk)
n.atoms ........................... 14
E(tot) ............................ -158.44960700
Hessian not found on file fcc
E(tot) - E(reference geom) ........ 24.06008200
The geometry is changed according to the FROZEN options
1. the follow. RICs are obtained by the current QM geom
2. the reference geom is changed accordingly
and the obtained geom is used in the follow
RIC -- atoms -- current refer change
1 1 2 3 4 -0.000 -180.000 180.000
WARNING: the following RICs are changed too much
FrozGeo RelaxGe change allowed
14 113.394 116.838 -3.444 1 2 3 0 3.000 1.148
20 113.394 116.838 -3.444 2 3 4 0 3.000 1.148
--- GEOMETRY from frozen changes (angstrom) ---
x y z Nucl.ch
1 C1 -0.4740072 -2.1583107 0.0012238 3.2
2 C2 1.0561133 -2.1764456 0.0021622 3.2
3 C3 1.6478863 -3.5900924 -0.0001270 3.2
4 C4 0.5869913 -4.6928581 -0.0028806 3.2
5 H5 -0.8678333 -1.1289935 0.0029178 0.5
[...]
As an example, in the above frame is reported the information printed by JOYCE, concerning the first of the n-butane non equilibrium geometries (given in the $scan section).
In this geometry, the carbon backbone dihedral was displaced to 0 , i.e.
in a cis conformation, but similar information is printed in the output for all other scanned geometries.
In the first block, information about the QM level of theory is printed, together with the computed absolute energy and the energy difference (E(scf) - E(reference geom) in kJ/mol) with the absolute minimum (geometry 0 in the , i.e.
in a cis conformation, but similar information is printed in the output for all other scanned geometries.
In the first block, information about the QM level of theory is printed, together with the computed absolute energy and the energy difference (E(scf) - E(reference geom) in kJ/mol) with the absolute minimum (geometry 0 in the 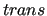 conformation).
In this case the latter is conformation).
In this case the latter is  24 kJ/mol.
Next, the scanned RIC is specified together with some information about the employed FIRA approximation, explained in some detail in section 7.2.5.
If the value of any RIC, other than the scanned one, results to be much different in the current scanned geometry with respect of the reference (absolute minimum) one, JOYCE gives a warning and prints the difference between the two values.
Particular attention should be paid to this info in case an atom pair interacting through nonbonded interactions appears in this list. If so, please resort to the 24 kJ/mol.
Next, the scanned RIC is specified together with some information about the employed FIRA approximation, explained in some detail in section 7.2.5.
If the value of any RIC, other than the scanned one, results to be much different in the current scanned geometry with respect of the reference (absolute minimum) one, JOYCE gives a warning and prints the difference between the two values.
Particular attention should be paid to this info in case an atom pair interacting through nonbonded interactions appears in this list. If so, please resort to the 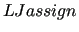 keyword as detailed in Section 5.1.
In the previous frame, for example, RICs number 14 and 20, i.e. the bending angles
the two Carbon atoms triplets (1,2,3 and 2,3,4) change together with the scanned dihedral, passing from keyword as detailed in Section 5.1.
In the previous frame, for example, RICs number 14 and 20, i.e. the bending angles
the two Carbon atoms triplets (1,2,3 and 2,3,4) change together with the scanned dihedral, passing from 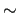 113 113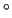 (in the trans minimum energy reference geometry) to (in the trans minimum energy reference geometry) to 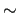 117 117 (in the current cis conformation).
Finally, the geometry created through the FIRA and effectively employed in the parameterization is printed for reference. (in the current cis conformation).
Finally, the geometry created through the FIRA and effectively employed in the parameterization is printed for reference.
When the loop on all geometries is over, JOYCE3.0 starts the QMD-FF parameterization, solving the system of equations to find the best linear parameters as reported in equations (35)-(45).
The results are summarized in section F) of the output as follows.
----------------
F) QMD-FF parameterization
----------------
=================================================
S O L V E T H E L I N E A R S Y S T E M
F O R T H E B E S T P A R A M E T E R S
=================================================
n. of parameters .............. 48
n. of points .................. 680
------ read dependences ------
1 param 44 = param 43 * 1.0000
2 param 45 = param 43 * 1.0000
3 param 46 = param 43 * 1.0000
4 param 47 = param 43 * 1.0000
5 param 48 = param 43 * 1.0000
---- read assigned parameters ----
---- Expected input units: ----
---- [L] =A ; [E] = kJ/mol ----
- all nonbonded prms have been assigned -
---- Expected input units: ----
---- [L] =A ; [E] = kJ/mol ----
1 param 1 = 0.24046 input = 2254.5152
2 param 2 = 0.22723 input = 2130.5117
3 param 3 = 0.24046 input = 2254.5152
[...]
35 param 35 = 0.11934 input = 313.3363
36 param 36 = 0.11934 input = 313.3363
37 param 37 = 0.11934 input = 313.3363
First, J OYCE looks whether assigned parameters or dependencies were given in the input, through the $assign or $dependencies commands.
If so, all read assignments are printed out, as shown in the frame below.
Please note that the parameter number always refers to the order given in the topology file, where the RIC spanning the FF are defined.
The linear system is solved using the Single Value Decomposition (SVD) algorithm, [ 1]
after J OYCE has constructed 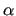 and 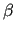 matrices (see section 7.2.3) from the information reported in all above frames, considering the imposed constraints and/or dependencies.
Further details about the numerical procedure are also printed by the program, as shown in the next frame.
After the number of free parameters has been written, the effective threshold (as set in the $zero environment in the input file) and the eigenvalues consequently discarded are reported in some detail, which can be increased by setting the proper print level through the  keyword.
Number of free parameters ......... 6
given threshold for null eigenvalues .... 0.100D-11 * Max(eigenvalue)
maximum value of the A matrix ........... 0.357D+01
both A and B are multiplied by .......... 0.100D+01
sum (over points) of the weights ........ 0.100D+02
first kept metric eigenvalues from 43
7.749D-02 1.081D-01 1.081D-01 3.691D-01 1.773D+00
metric eigensolution n. 42 0.000000
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
[...]0.00 0.00 0.00 0.00 0.00 0.00 0.00 1.00
metric eigensolution n. 43 0.7749045E-01
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
[...]
0.00 0.00 0.00 0.00 0.00 0.00 0.00 -0.76 0.27 0.37
0.27 0.37 0.00 0.00 0.00 0.00 0.00 0.00
Max err in the matrix inversion 1.00
for the matrix element 1 1
Due to the empirical nature of this threshold, it is requisite, at least in the preliminary runs, to check if the selected values is adequate to discard only the null eigenvalues.
To aid this task, as appears in the above frame, J OYCE prints the first discarded eigenvalue and the first one kept.
As displayed in the next frame, JOYCE3.0 prints a summary of the best parameters final values (both in atomic and standard units),
specifying if the constants was assigned, dependent or free to vary.
In the latter case the program also computes and writes a "sensitivity index" (which is set to zero in the former cases), that gives some indication whether the selected RIC is connected to the scanned one.
==== VALUE OF THE BEST LINEAR PARAMETERS ====
# param.s 48 #. of free param.s 11
sensitivity index: =1 OK, =0 useless function
-----------------------
# value Sens Index
1 0.240460 0.000 C1-C2
2 0.227234 0.000 C2-C2
3 0.240460 0.000 C1-C2
4 0.330646 0.000 C1-H1
5 0.330646 0.000 C1-H1
6 0.330646 0.000 C1-H1
7 0.319339 0.000 C2-H2
8 0.319339 0.000 C2-H2
9 0.319339 0.000 C2-H2
[...]
13 0.330646 0.000 C1-H1
14 0.270664 0.000 C1-C2-C2
15 0.132040 0.000 C2-C1-H1
[...]
37 0.119343 0.000 H1-C1-H1
38 -0.000750 1.000 C1-C2-C2-C1_n=0
39 0.001676 1.000 C1-C2-C2-C1_n=1
40 0.000672 1.000 C1-C2-C2-C1_n=2
41 0.002879 1.000 C1-C2-C2-C1_n=3
42 0.000059 1.000 C1-C2-C2-C1_n=4
43 0.000820 1.000 H1-C1-C2-C2_n=3
[...]
48 0.000820 1.000 H1-C1-C2-C2_n=3
TOTAL STANDARD DEVIATION 0.189D-04 atomic units
Once they have been determined, all the best parameters ( i.e. force constants and equilibrium coordinates) are also printed in a output topology file.
This file is named by default joyce.new.top, and as already mentioned is directly printed in the G ROMACS .top format.
This file is the main JOYCE output and it can be used by the GROMACS engine[18] to start a MD simulation on the target molecule.
When the fitting procedure is ended, the above mentioned information is also printed in the J OYCE output as follows:
RESULTS OF THE LINEAR FITTING (kJ/mol L=angst)
exact computed residue Chisq
1 0.0029 0.0034 -0.0004 0.00000 hes 0 1 1 0.0271
2 0.0000 0.0002 -0.0002 0.00000 hes 0 2 1 0.0135
3 0.0101 0.0113 -0.0011 0.00000 hes 0 2 2 0.0271
4 0.0000 0.0000 -0.0000 0.00000 hes 0 3 1 0.0135
5 0.0000 -0.0000 0.0000 0.00000 hes 0 3 2 0.0135
[...]665 0.0000 -0.0000 0.0000 0.00018 hes 0 36 35 0.0135
666 1.8658 1.8734 -0.0076 0.00018 hes 0 36 36 0.0271
667 24.0601 23.8180 0.2420 0.00039 Energy- 1 0.0360
668 14.1016 14.5547 -0.4532 0.00113 Energy- 2 0.0360
669 3.9908 3.6221 0.3687 0.00162 Energy- 3 0.0360
670 8.0787 8.3319 -0.2533 0.00185 Energy- 4 0.0360
671 14.4770 14.3392 0.1378 0.00192 Energy- 5 0.0360
[...]
679 6.1122 6.3630 -0.2508 0.00258 Energy-13 0.0360
680 0.0026 -0.0972 0.0998 0.00262 Energy-14 0.0360
TOTAL STANDARD DEVIATION 5.118D-02 kJ/mol L=angst
The above frame shows the results obtained for the n-butane molecule, where the standard deviation with respect to J OYCE's objective function ( 35) is reported together with a detailed list of the fitting results.
With respect to the notation of equation ( 35), the point number is reported in the first column, while in the sixth and seventh column the point type (energy, gradient or Hessian) and the 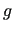 geometry in which is computed are reported.
In the next two columns (8 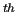 and 9 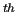 ) the 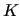 , 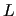 components are specified, while the given weights ( 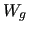 ,
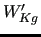 and
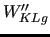 ) are shown in the last column in their normalized value.
The second to the fifth column report respectively the QM ( exact) energy (or gradient or Hessian), its FF value ( computed), the difference ( residue) between the formers and the partial mean square deviation ( Chisq).
Note that, starting form the J OYCE3.0 release, these results can also be saved in the graphical  format. Futher information can be found at the J OYCE website.[ 13]
After the fitting procedure is complete, the program computes the QMD-FF mass weighted Hessian matrix, its eigenvalues and the resulting frequencies based on the optimized force constants and the selected RIC. Next, it prints the data obtained according to the same format previuoly employed for the QM Hessian and frequencies, as appears from the next frame.
=====================================================
N O R M A L V I B R A T I O N A L M O D E S
by the optim. FF (EQUIL GEOMETRY)
=====================================================
Compute the Mass weighted Hessian
Diagonalize the Mass weighted Hessian
Eigenvalues of the (M-1/2)*F*M(-1/2) matrix (mH) by the optim. FF (EQUIL GEOMETRY)
1 0.2312E-03 2 0.1031E-02 3 0.1271E-02 4 0.2473E-02 5 0.3947E-02
6 0.1045E-01 7 0.1399E-01 8 0.1449E-01 9 0.1664E-01 10 0.1793E-01
11 0.1916E-01 12 0.1943E-01 13 0.2167E-01 14 0.2414E-01 15 0.3255E-01
16 0.3306E-01 17 0.3905E-01 18 0.4184E-01 19 0.4193E-01 20 0.4245E-01
21 0.4384E-01 22 0.4401E-01 23 0.4416E-01 24 0.4603E-01 25 0.4683E-01
26 0.5164E-01 27 0.1851 28 0.1861 29 0.1870 30 0.1873
31 0.1932 32 0.1938 33 0.2005 34 0.2006 35 0.2006
36 0.2007
Frequencies in 1/cm by the optim. FF (EQUIL GEOMETRY)
1 105.525 2 222.870 3 247.413 4 345.160 5 436.034
6 709.555 7 820.973 8 835.406 9 895.274 10 929.307
11 960.774 12 967.534 13 1021.706 14 1078.266 15 1252.237
16 1261.962 17 1371.433 18 1419.699 19 1421.226 20 1429.891
21 1453.150 22 1455.915 23 1458.527 24 1489.027 25 1501.971
26 1577.162 27 2986.119 28 2993.868 29 3001.550 30 3004.034
31 3050.301 32 3055.482 33 3107.927 34 3108.391 35 3108.760
36 3109.380
Similarly to the QM normal analysis carried out in the previous sections, the QMD-FF normal modes projection over the RICS is printed in the same format used for their QM counterparts, as briefly shown in the next frame.
VIBRATIONAL NORMAL MODES: Int.Coord. displac.s by the optim. FF (EQUIL GEOMETRY)
105.5 222.9 247.4 345.2 436.0 ...
1 2 3 4 5 ...
1 C1-C2 0.000 0.000 0.000 0.003 -0.033 ...
2 C2-C2 0.000 0.000 0.000 0.000 -0.037 ...
3 C2-C1 0.000 0.000 0.000 -0.003 -0.033 ...
14 C1-C2-C2 0.000 0.000 0.000 -0.066 -0.043 ...
15 C2-C2-C1 0.000 0.000 0.000 0.066 -0.043 ...
16 C2-C1-H1 0.000 0.000 0.000 0.016 0.003 ...
[...]
3050.3 3055.5 3107.9 3108.4 3108.8 3109.4
31 32 33 34 35 36
4 C1-H1 0.000 0.000 0.000 0.000 -0.383 0.036
5 C1-H1 -0.012 0.010 -0.392 -0.101 0.193 -0.018
6 C1-H1 0.012 -0.010 0.392 0.101 0.193 -0.018
7 C1-H1 0.000 0.000 0.000 0.000 0.039 0.357
8 C1-H1 -0.008 -0.009 0.110 -0.360 -0.019 -0.179
9 C1-H1 0.008 0.009 -0.110 0.360 -0.019 -0.179
Finally, a brief comparison between QM and FF computed vibrational frequencies is printed, as shown in the next frame.
It is worth noticing that the indicated standard deviation is only for comparison purposes, as the fitting target is the minimization of equation (35).
Note also that the comparison between QM and FF frequencies is done on the base of the overlap of the corresponding normal modes (QM and FF), and not on the nearest value of the frequency itself.
=================================================
Compare Norm Modes from QM and FF
=================================================
iFF Freq/FF ig03 freq/g03 overl err
35 3108.8 36 3096.1 0.765 12.6
36 3109.4 35 3095.4 0.764 14.0
34 3108.4 34 3090.5 0.806 17.9
33 3107.9 33 3087.0 0.851 20.9
31 3050.3 32 3046.8 0.922 3.5
32 3055.5 31 3024.1 0.975 31.4
30 3004.0 30 3021.4 0.847 -17.3
29 3001.5 29 3019.9 0.866 -18.4
27 2986.1 28 3008.7 0.913 -22.6
28 2993.9 27 3002.0 0.910 -8.1
23 1458.5 26 1484.8 0.656 -26.3
18 1419.7 25 1478.3 0.668 -58.6
21 1453.2 24 1470.6 0.983 -17.4
22 1455.9 23 1468.8 0.991 -12.9
19 1421.2 22 1463.1 0.674 -41.8
24 1489.0 21 1459.9 0.842 29.1
25 1502.0 20 1399.0 0.686 102.9
26 1577.2 19 1398.0 0.779 179.2
20 1429.9 18 1387.4 0.693 42.5
15 1252.2 17 1320.7 0.947 -68.5
17 1371.4 16 1310.5 0.934 60.9
16 1262.0 15 1277.5 0.852 -15.5
13 1021.7 14 1197.1 0.986 -175.4
14 1078.3 13 1163.3 0.977 -85.0
10 929.3 12 1074.5 0.925 -145.2
9 895.3 11 1024.4 0.794 -129.2
11 960.8 10 976.4 0.785 -15.7
12 967.5 9 955.1 0.888 12.5
7 821.0 8 844.8 0.923 -23.9
8 835.4 7 809.4 0.967 26.0
6 709.6 6 741.8 0.984 -32.2
5 436.0 5 424.7 0.978 11.3
3 247.4 4 267.9 0.995 -20.5
4 345.2 3 257.7 1.000 87.4
2 222.9 2 228.4 0.991 -5.5
1 105.5 1 123.2 0.998 -17.7
Standard deviation (cm-1) 64.68
Note that if the $gracefreq keyword has been activated in the input file, the above results are also printed in an output file in the  format for a straightforward visualization.
Eventually, if the fitting was successfully performed, J OYCE log file should
always end with a NORMAL EXIT sentence.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]() label
label![]() .inp it is the user defined name of the related input file.
This file contains printouts and detailed information about all operations performed by the JOYCE code during the parameterization procedure.
The verbosity level of the printouts is set by the value assigned to the $print keyword in the joyce.molname.inp file.
Because of the many information it contains, the output file cannot be described in much detail in this manual.
Only some of the most important sample sections will here be illustrated. A careful reading of the output log file is highly recommended to JOYCE new users.
.inp it is the user defined name of the related input file.
This file contains printouts and detailed information about all operations performed by the JOYCE code during the parameterization procedure.
The verbosity level of the printouts is set by the value assigned to the $print keyword in the joyce.molname.inp file.
Because of the many information it contains, the output file cannot be described in much detail in this manual.
Only some of the most important sample sections will here be illustrated. A careful reading of the output log file is highly recommended to JOYCE new users.