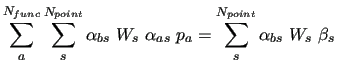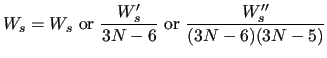The optimal parameters of the Force Field
The best FF parameters in order to represent the
internal molecular motion are obtained by minimizing the following objective function, written as a sum over the considered molecular geometries
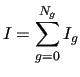 |
|
|
(34) |
where
![$\displaystyle I_g = W_g \left[ (E_g-E_0) - V_g \right]^2 +
\sum _{K=1}^{3N-6} \frac{W_{Kg}^{\prime}} {3N-6}
\left[ E_{Kg}^{\prime} -V_{Kg}^{\prime}\right] ^{2} +$](img211.png) |
|
|
|
![$\displaystyle \sum_{K\leq L}^{3N-6} \frac{2W_{KLg}^{\prime\prime}}{(3N-6) (3N-5) }
\left[ E_{KLg}^{\prime\prime}-V_{KLg}^{\prime\prime }\right] ^2$](img212.png) |
|
|
(35) |
The indexes  (capital letters) run over the normal coordinates and include all the modes except for the rotational and translational ones.
(capital letters) run over the normal coordinates and include all the modes except for the rotational and translational ones.
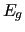 is the total energy obtained by a QM calculation and
is the total energy obtained by a QM calculation and
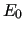 is the same at the reference geometry (
is the same at the reference geometry ( ).
).
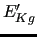 (
(
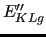 ) is the energy gradient (Hessian) at a given geometry with respect to the NC evaluated at the same geometry.
) is the energy gradient (Hessian) at a given geometry with respect to the NC evaluated at the same geometry. 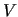 ,
,
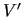 and
and
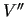 are the corresponding quantities calculated by the FF in equation (6).
The constants
are the corresponding quantities calculated by the FF in equation (6).
The constants 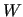 ,
,
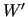 and
and
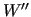 weight the several terms at each geometry and can be chosen in order to drive the results depending on the circumstances.
The energy, gradient and Hessian terms are normalized in order to account for the different number of terms and to make the weights independent from the number of atoms in the molecule.
weight the several terms at each geometry and can be chosen in order to drive the results depending on the circumstances.
The energy, gradient and Hessian terms are normalized in order to account for the different number of terms and to make the weights independent from the number of atoms in the molecule.
To compute the energy derivatives entering the merit function (35) we have to perform some transformations since no derivative is originally
expressed with respect to the NCs.
Indeed standard quantum chemistry programs
provide derivatives
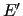 and
and
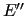 with respect to CCs.
Using the above relations and exploiting the completeness of the CCs, the transformation is simple
with respect to CCs.
Using the above relations and exploiting the completeness of the CCs, the transformation is simple
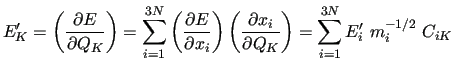 |
|
|
(36) |
or, in matrix form
![$\displaystyle [E^{\prime}]_{NC} = \widetilde{C} M^{-1/2} [E^{\prime}]_{CC}$](img227.png) |
|
|
(37) |
where the square parentheses indicates column vectors of energy gradients computed with respect to the NCs and the CCs.
The FF energy gradients at a given geometry
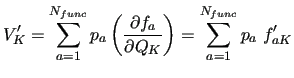 |
|
|
(38) |
can be conveniently computed using the derivatives of the basis function with respect to the RICs, that is
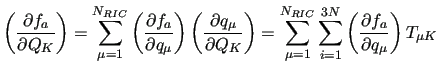 |
|
|
(39) |
or in matrix form
![$\displaystyle [f_a^{\prime}]_{NC} = \widetilde{T} [ f_a^{\prime }]_{RIC}$](img230.png) |
|
|
(40) |
The Hessian matrix of the QM calculation in NCs
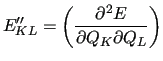 |
|
|
(41) |
is obtained from the Hessian matrix in the CC basis according to
![$\displaystyle [E^{\prime\prime}]_{NC} = \widetilde{C} M^{-1/2} [E^{\prime\prime}]_{CC}
M^{-1/2} C$](img232.png) |
|
|
(42) |
The second derivatives of the FF are a bit more complicated since they involve
derivatives of the 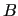 matrix and are conveniently expressed in explicit
form
matrix and are conveniently expressed in explicit
form
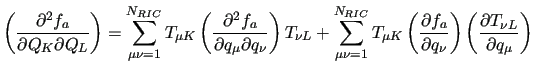 |
|
|
(43) |
As shown in equation (6), the FF is linear
in the 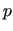 parameters, thus the least squares
minimization of functional (35)
can be written as
parameters, thus the least squares
minimization of functional (35)
can be written as
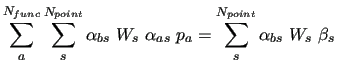 |
|
|
(44) |
where the index 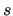 runs over the collections
runs over the collections
![$ [g]$](img237.png) ,
, ![$ [Kg]$](img238.png) and
and ![$ [KLg]$](img239.png) defined in equation (35)
for energy, gradient and Hessian, respectively.
Following this notation
the matrix
defined in equation (35)
for energy, gradient and Hessian, respectively.
Following this notation
the matrix 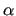 and the vector
and the vector 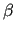 are defined as
are defined as
and
where 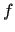 's are the functions of equation (6),
's are the functions of equation (6), 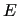 ,
,
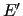 ,
,
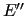 the QM data and
the QM data and 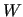 ,
,
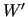 ,
,
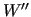 the weights
of the merit function (35).
Thus, defining
the weights
of the merit function (35).
Thus, defining
one has to solve a standard linear equation in the form
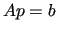 |
|
|
(45) |
where 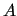 is a symmetric matrix.
is a symmetric matrix.
In usual FF it is convenient for practical purposes, to employ functions of the RIC that will be in general redundant over the considered points.
The scalar product between the FF functions is defined as
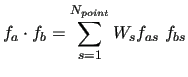 |
|
|
(46) |
and the redundancy strongly depends on the number and type of points included in the fitting.
However in general the 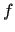 set might not be linearly
independent.
This leads to a singular
set might not be linearly
independent.
This leads to a singular 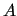 matrix and the direct inversion method can not be used to solve the linear system (45).
On the contrary, the Singular Value Decomposition method [37,38] adapted to symmetric matrices
is adequate and provides a stable solution of the linear system.
matrix and the direct inversion method can not be used to solve the linear system (45).
On the contrary, the Singular Value Decomposition method [37,38] adapted to symmetric matrices
is adequate and provides a stable solution of the linear system.
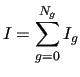
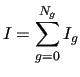
![]() and
and
![]() with respect to CCs.
Using the above relations and exploiting the completeness of the CCs, the transformation is simple
with respect to CCs.
Using the above relations and exploiting the completeness of the CCs, the transformation is simple
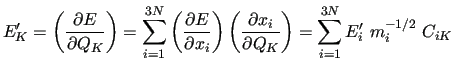
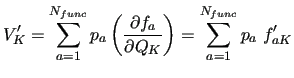
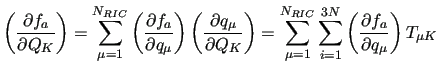
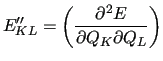
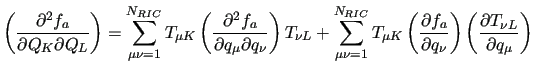
![]() parameters, thus the least squares
minimization of functional (35)
can be written as
parameters, thus the least squares
minimization of functional (35)
can be written as