In many molecular simulations a group of atoms whose individual behavior is considered not to be crucial for the properties to be investigated, can be grouped in a single interaction site. This approach, henceforth named United
Atom (UA), allows for saving computational time and simultaneously removes some high frequency vibrational modes which can limit the integration time step in MD simulations.
The most common example concerns aliphatic chains where each CH![]() group is treated as a single interaction site (C
group is treated as a single interaction site (C![]() ) with FF parameters accounting for the effect of the hydrogen atoms both in the non-bonded interactions and electrostatic charge.
Despite recent work has been done
for some torsional potentials, usually the
intramolecular FF parameters of "stiff" IC are not changed in the UA approach, thus the parameters driving the C
) with FF parameters accounting for the effect of the hydrogen atoms both in the non-bonded interactions and electrostatic charge.
Despite recent work has been done
for some torsional potentials, usually the
intramolecular FF parameters of "stiff" IC are not changed in the UA approach, thus the parameters driving the C![]() -C
-C![]() -C
-C![]() stretching and bending motion in the aliphatic chains are the same as those commonly employed in the FA description.
stretching and bending motion in the aliphatic chains are the same as those commonly employed in the FA description.
In the UA approximation the involved atoms are considered to move as a single point with the consequence that the translational movements with respect to the rest of the molecule can be somehow taken into account, but the relative rotational movements are irreparably lost. In other words a three dimensional object described by 6 coordinates is transformed into a single point described by 3 coordinates. Even in the (non realistic) hypothesis that there exists some local vibrational modes much faster than those involving the atoms close to the UA, this approximation affects the motion of the neighboring atoms. Thus the remaining vibrational frequencies are altered by the UA approach and it is convenient focusing on the representation of the intra-molecular potential energy rather than on the vibrational analysis.
In the JOYCE program the UA atom approach, consistently with the previous FA approach, is treated on the basis of ab initio calculation of energies,
gradients and Hessian.
The main problem concerns with the transformation of
the gradient vector and Hessian matrix in equation (35) in the case the number of effective atoms is less than than the number of true atoms in the molecule.
Let consider for simplicity the case of a single UA in which ![]() atoms are grouped together.
We use the indeces
atoms are grouped together.
We use the indeces ![]() for the Cartesian coordinates
referred to the atoms involved in the UA and the indeces
for the Cartesian coordinates
referred to the atoms involved in the UA and the indeces ![]() for those of the remaining atoms not involved in the UA (in this section we are forced to change the previous notation).
For simplicity we suppose that only one atom in the UA group is linked to the unaltered atoms.
The first order energy expansion around a given geometry is
for those of the remaining atoms not involved in the UA (in this section we are forced to change the previous notation).
For simplicity we suppose that only one atom in the UA group is linked to the unaltered atoms.
The first order energy expansion around a given geometry is
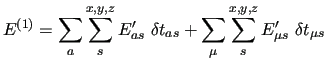 |
(47) |
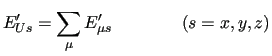 |
(48) |
The second order energy is
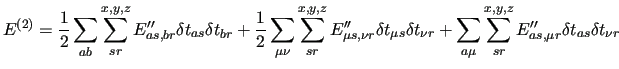 |
(49) |
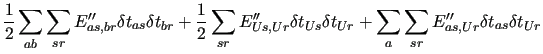 |
|||
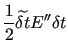 |
(52) |
It is easy to verify that such a transformation of the Hessian matrix will preserve the three null eigenvalues due to translations, whereas the rotational modes of a molecule with UA included may lead to small (unphysical) energy contributions with the further undesirable consequence of small mixing between rotational and vibrational modes.
The two other quantities of the UA to be defined are the mass and the position. For most of standard UAs (e.g. methylene and methyl groups) the mass is taken as the sum of the involved atoms. In the case only one atom of the grouped atoms forms bonds with the rest of molecule, the natural choice for the position seems to make the UA coincident with that atom. However other choices are possible, for example the UA may be placed in the center of mass of the grouped atoms at the equilibrium geometry and/or its mass may be chosen in order to preserve the original inertia moments. Taking as criteria the magnitude of the rotational eigenvalues and the perturbation of the vibrational modes, these attempts do not lead to any improvement and were rejected. With the original choice the rotational eigenvalues at the equilibrium geometry are found to be much lower than the low frequency vibrational modes and the contamination is very small.
In summary the UA approach preserves some of the original atom-atom interactions contained in the Hessian matrix and leads to a useful simplification of the intra-molecular energy hyper-surface but does not allow conserving the rigorous implementation of the all-atom force field presented in this paper.