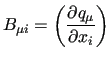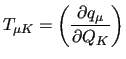Since the Hessian and gradients are computed in CCs, whereas the FF is usually expressed through RICs, some coordinate transformation is required.
For infinitesimal displacements with respect to a given geometrical conformation, the RICs are related to the nuclear CCs 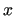 through a non invertible transformation
through a non invertible transformation
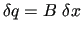 |
|
|
(25) |
where 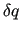 and
and 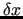 are colum vectors. The Wilson rectangular
are colum vectors. The Wilson rectangular 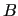 matrix
matrix
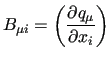 |
|
|
(26) |
is related to the geometry the displacements are referred to, and can be accurately computed both in
analytical [36] and numerical ways.
The normal coordinates are computed from the Hessian matrix in CCs
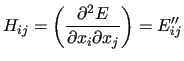 |
|
|
(27) |
obtained by a QM calculation at a given geometry. 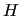 is transformed to the mass weighted CCs form and diagonalized by a unitary matrix
is transformed to the mass weighted CCs form and diagonalized by a unitary matrix 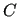
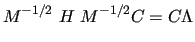 |
|
|
(28) |
The matrix 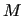 is diagonal and for each CC contains the mass
is diagonal and for each CC contains the mass 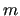 of the related atom.
The columns of the
of the related atom.
The columns of the 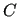 matrix are the linear combinations of
the mass weighted CCs that correspond to the NCs displacements
matrix are the linear combinations of
the mass weighted CCs that correspond to the NCs displacements
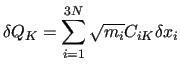 |
|
|
(29) |
or in matrix form
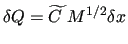 |
|
|
(30) |
where  and
and 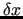 are column vectors.
In the case the geometry corresponds to an absolute or local energy minimum,
are column vectors.
In the case the geometry corresponds to an absolute or local energy minimum, 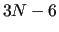 eigenvalues
eigenvalues
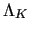 are positive and refer to vibrations, whereas the 3 translational and 3 rotational modes are identified by zero eigenvalues.
In other cases negative eigenvalues can occur and these do not correspond to vibrational modes.
If all the NCs are retained, the transformation of equation (29) is fully invertible
are positive and refer to vibrations, whereas the 3 translational and 3 rotational modes are identified by zero eigenvalues.
In other cases negative eigenvalues can occur and these do not correspond to vibrational modes.
If all the NCs are retained, the transformation of equation (29) is fully invertible
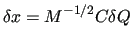 |
|
|
(31) |
The relation between the RICs and the NCs can be easily obtained exploiting the completeness of the CCs basis set. Using equations (25) and (31)
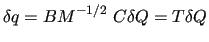 |
|
|
(32) |
where the 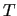 matrix is defined as
matrix is defined as
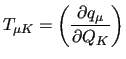 |
|
|
(33) |
Thus the RICs may be expressed in terms of the NCs and the inclusion or not of the rotational and translational modes is uninfluential since they leave the RICs unchanged.
![]() through a non invertible transformation
through a non invertible transformation