To make the formulae easier to be understood,
the following notation will be
adopted for the summation indexes and symbols
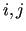 are used for the Cartesian coordinates (CCs)
are used for the Cartesian coordinates (CCs) 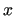 or
mass weighted Cartesian coordinates (
or
mass weighted Cartesian coordinates (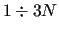 )
)
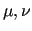 indicate the redundant internal
coordinates [33,34] (RICs)
indicate the redundant internal
coordinates [33,34] (RICs)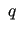 (
(
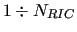 )
)
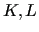 run over the normal coordinates (NCs)
run over the normal coordinates (NCs) 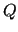 (
(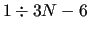 ) (
) (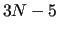 for linear molecules)
for linear molecules)
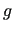 run over the considered molecular geometries (
run over the considered molecular geometries (
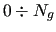 )
)
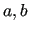 indicate the functions
indicate the functions 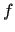 used to represent the empirical
FF and/or the number of linear parameters of the FF (
used to represent the empirical
FF and/or the number of linear parameters of the FF (
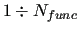 )
)
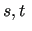 run over the quantities to be represented by the FF
(energies, energy gradients and Hessian) for the considered
geometries (
run over the quantities to be represented by the FF
(energies, energy gradients and Hessian) for the considered
geometries (
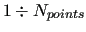 )
)
The target FF, to be used in molecular dynamics or molecular mechanics, is expressed through the linear combination of functions 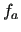 of a set of RICs as in equation (12), with or without the coupling term (13).
The functions
of a set of RICs as in equation (12), with or without the coupling term (13).
The functions 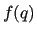 entering these equations may conveniently be expressed in terms of displacements with respect to a given reference geometrical conformation identified by the vector
entering these equations may conveniently be expressed in terms of displacements with respect to a given reference geometrical conformation identified by the vector 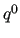
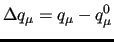 |
|
|
(24) |
Usually the RICs consist in all bond stretches, angle bendings and dihedral torsions that
can be obtained from a given connectivity criteria referred to the reference
conformation. The inversion coordinate [35] can be included for
atoms bonded to three other atoms. Non-bonded intramolecular interactions can also be added
in order to make the FF more accurate. In usual FFs the number of RICs
exceeds 3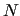 -6
and therefore they form a redundant set of coordinates. Although equation (6) has been written in general form, each function
-6
and therefore they form a redundant set of coordinates. Although equation (6) has been written in general form, each function 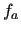 only depends on one or two RICs,
as reported in detail n equations (7)-(23).
only depends on one or two RICs,
as reported in detail n equations (7)-(23).
![]() of a set of RICs as in equation (12), with or without the coupling term (13).
The functions
of a set of RICs as in equation (12), with or without the coupling term (13).
The functions ![]() entering these equations may conveniently be expressed in terms of displacements with respect to a given reference geometrical conformation identified by the vector
entering these equations may conveniently be expressed in terms of displacements with respect to a given reference geometrical conformation identified by the vector ![]()