Internal Coordinates

Broadly speaking, the FF model intramolecular potential $V^{intra}_K$ is a function of a set $\{Q_1,Q_2, ..., Q_{N_K}\}$ of generalized (nuclear) internal coordinates (IC) describing target molecule $K$. Within the JOYCE procedure, the selection of this set is either automatically performed by the program or defined by the user, once the model (i.e. the definition of all interaction sites) mimicking the target molecule has been chosen. It is worth noticing that the selected IC are not necessarily required to be linearly independent, but redundant ($N_K$ $>$ 3$N_{sites}$ - 6) set of internal coordinates (RIC) can also be employed.

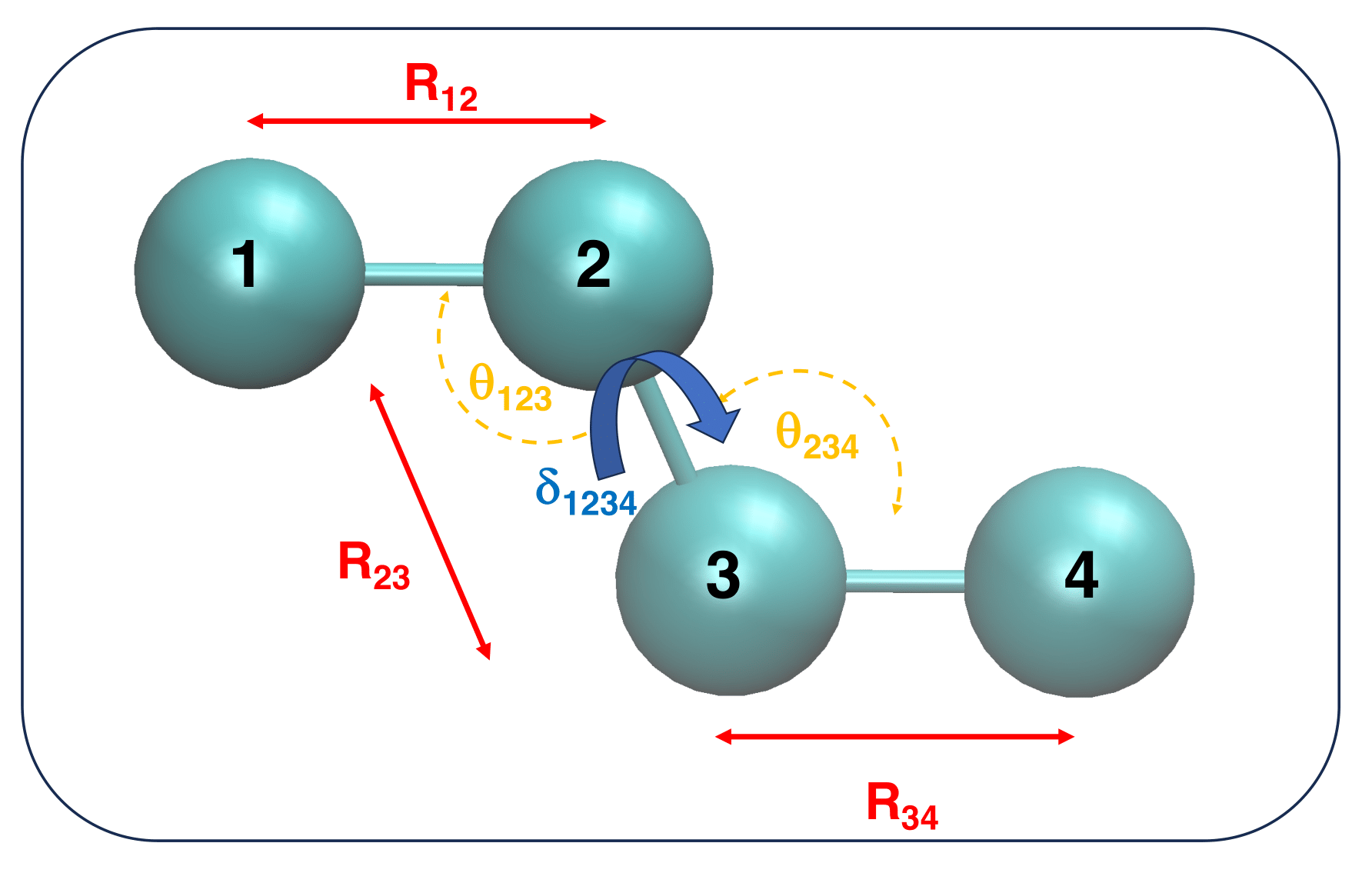
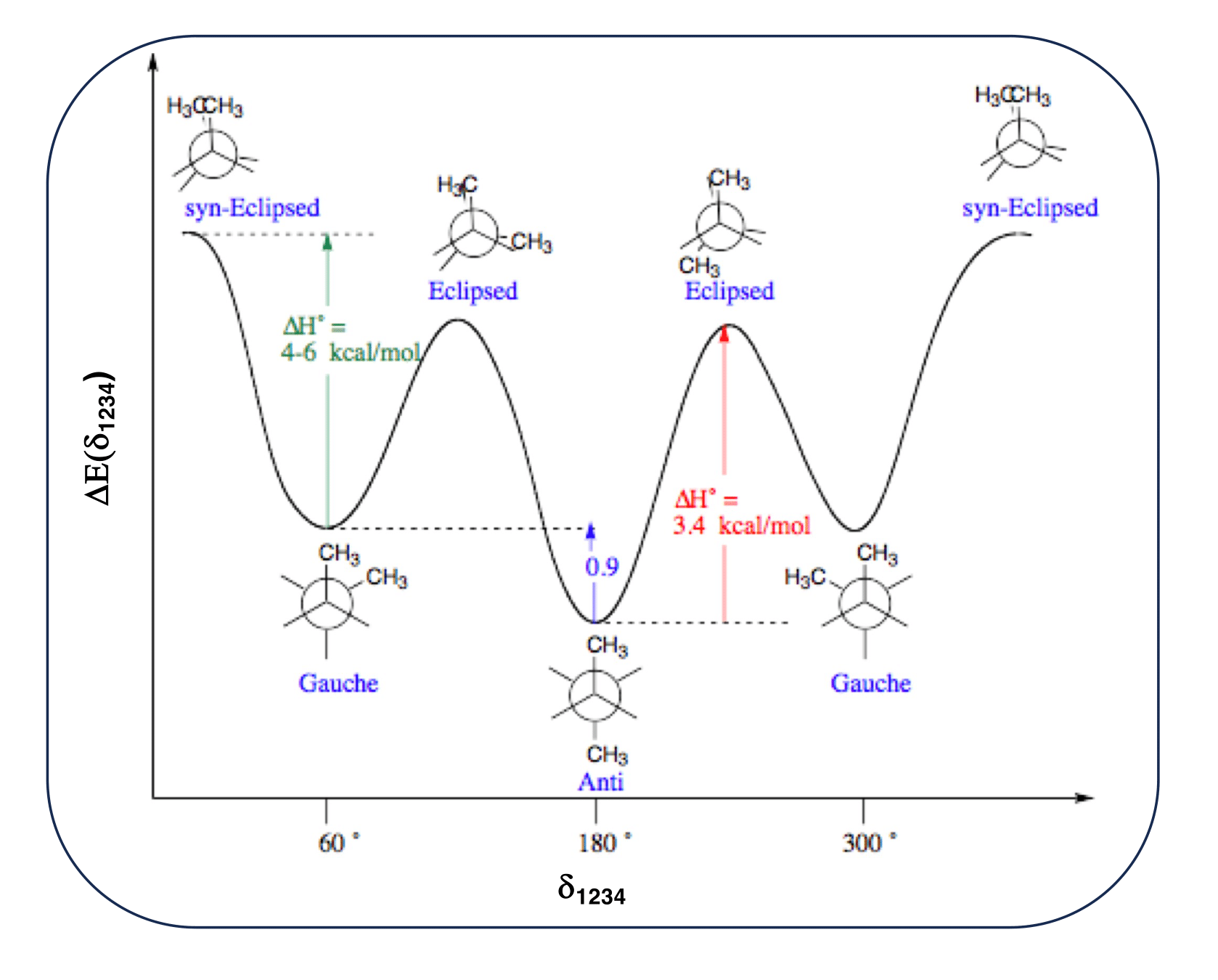
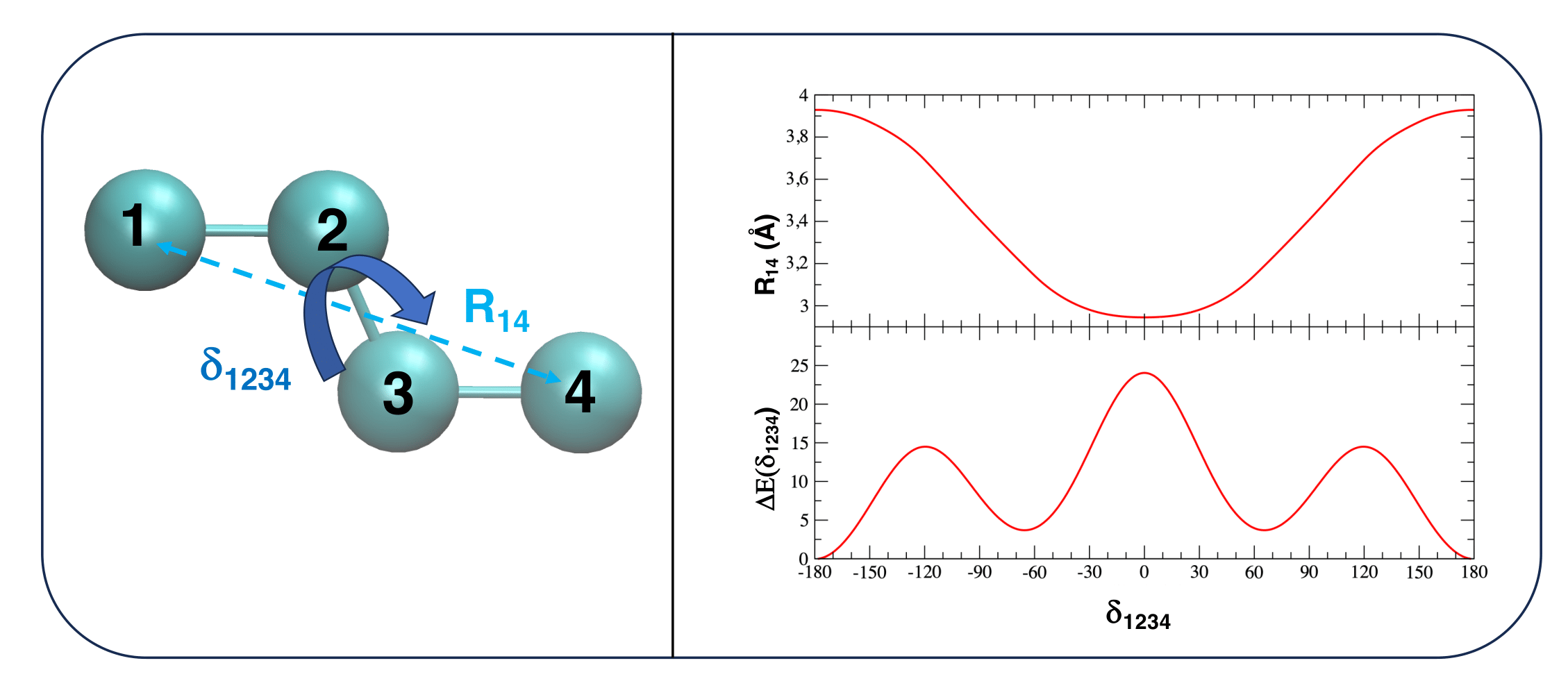
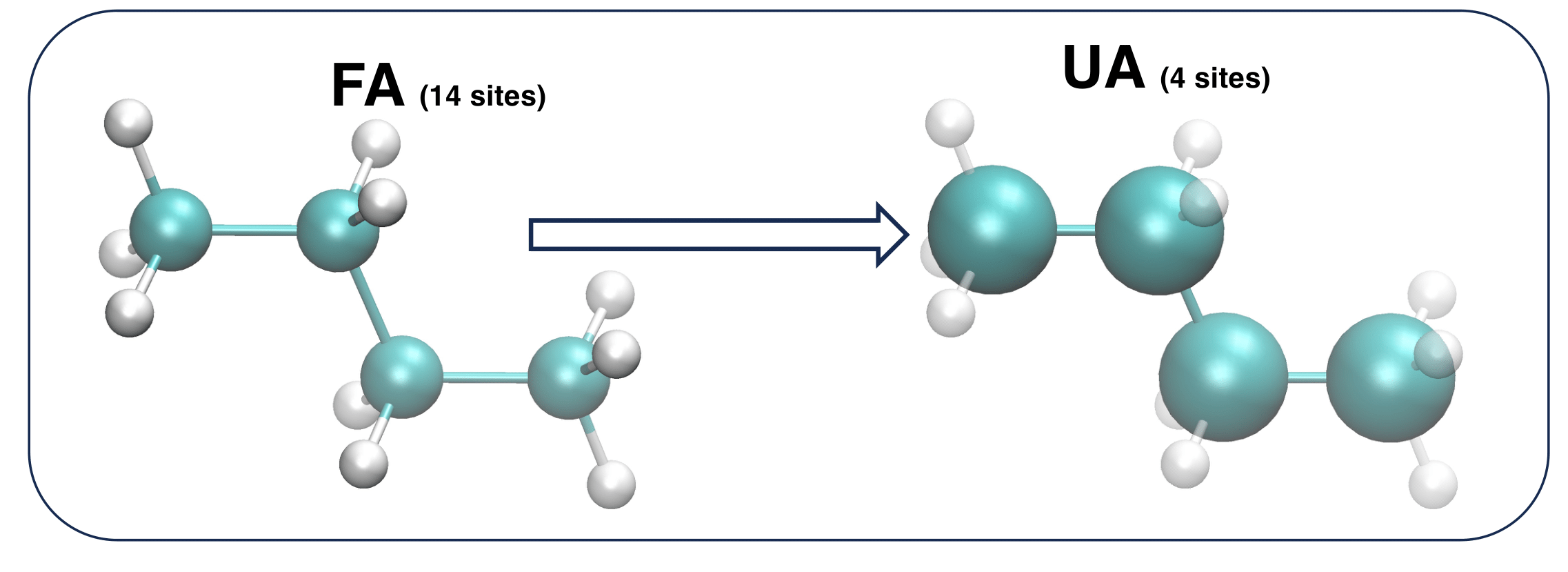
As an example, let's consider the n-butane molecule. For the sake of clarity, let's also suppose to adopt an united atom (UA) representation, where all Hydrogen atoms are grouped in an unique interaction site with the Carbon atom bonded to them. Within this model, sketched in Figure 2, the model n-butane molecule is composed by $N_{sites}$ = 4 interaction sites, whose geometry is completely described by (3$N_{sites}$ - 6)=6 IC.

Figure 2: UA model of the n-butane molecule. The number of interaction sites is reduced to four, which are completely described by six natural internal coordinates.

A natural choice for the minimal set of IC is reported in Figure 3, where the three bond lengths (R$_{1-2}$, R$_{2-3}$ and R$_{3-4}$), two bond angles ( $\theta_{1-2-3}$ and $\theta_{1-2-3}$) and the torsional dihedral ( $\delta_{1-2-3-4}$) are evidenced with different colors.

Figure 3: 6 natural IC for n-butane molecule: three bond lengths (R$_{12}$, R$_{23}$ and R$_{34}$), two bond angles ( $\theta _{123}$ and $\theta _{123}$) and the torsional dihedral ( $\delta _{1234}$) are evidenced by red, orange and blue lines, respectively.

Among these IC, it is convenient to distinguish between "stiff" and "soft" degrees of freedom,[1,21,32] highlithed in Figure 3 with reddish and blueish colors, respectively. Bond lengths and angles are intrinsically connected to stretching and bending motions, which are relatively high energy motions, usually characterized by small displacements from their equilibrium values. These types of coordinates will be classified as stiff. Conversely the rotation around the central bond,

Figure 4: Torsional energy profile for the n-butane molecule.

can be considered as a soft coordinate, since the internal energy profile, as a function of $\delta$, is characterized (see Figure 4) by the presence of local minima, separated by relatively low energy barriers. This coordinate can be subjected to large amplitude oscillations, eventually leading to the population of different trans and gauche minima, even at room temperature [1]).

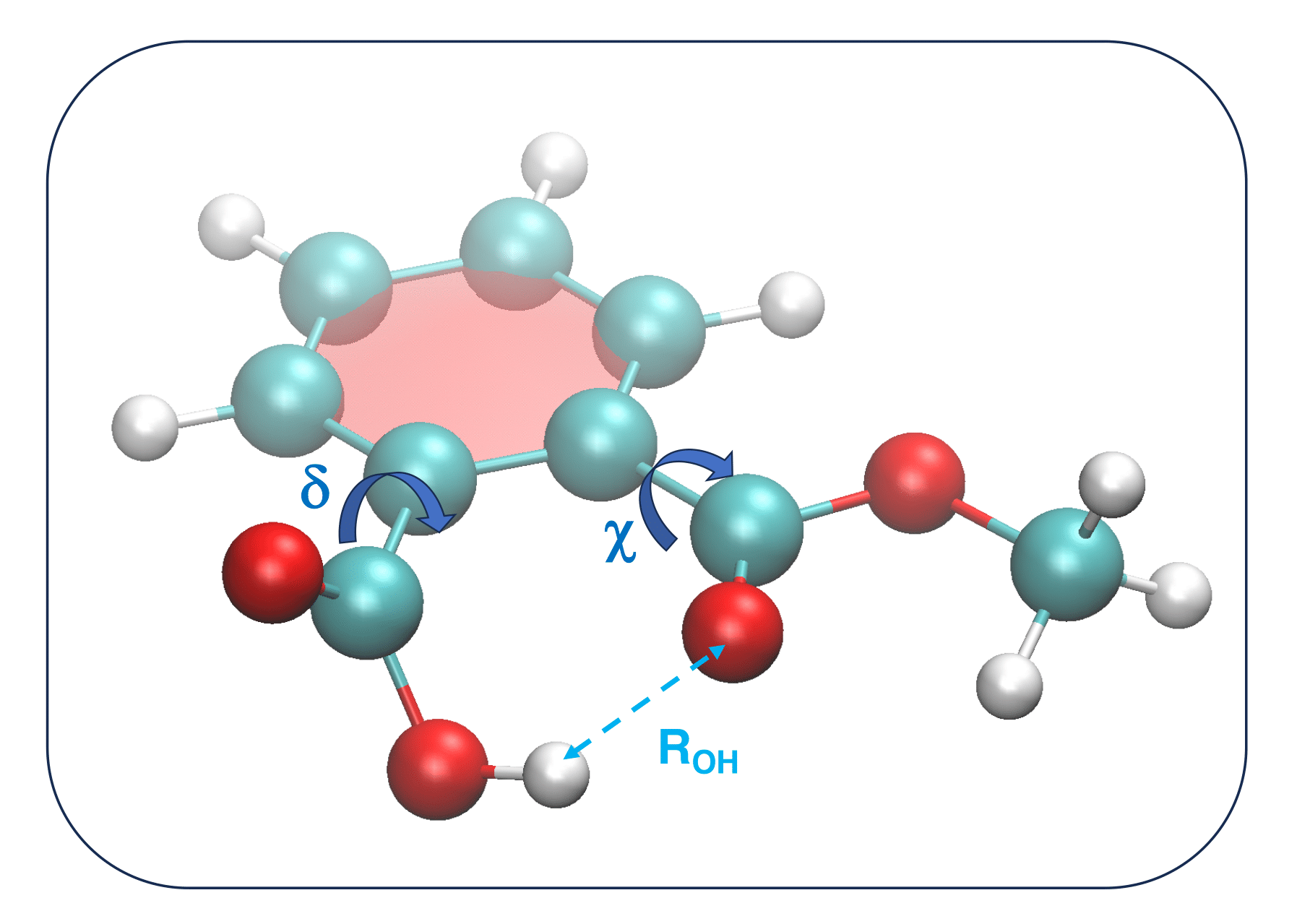
Another type of soft coordinate is the intramolecular distance between a pair of atoms connected by more than two bonds. Despite internal distances are intrinsically redundant (in that they can be expressed as a function of bond lengths, angles and dihedrals defining the relative position of the two atoms defining them), they turn out to be very useful in the case of large molecules, when important interactions between two different molecular regions take place after some geometrical rearrangement. Conversely, their use for smaller molecules does not seem to yield any particular advantage. As an example let's consider two different molecules, namely the PMME-H molecule and n-butane.

Figure 5: Torsional energy profile and 1-4 internal distance as a function of torsional dihedral $\delta$ for the n-butane molecule.

In the latter case, the $R_{14}$ intramolecular distance could be chosen as an adjunctive generalized coordinate. As shown in Figure 5, this distance is strongly dependent on the torsional dihedral $\delta$: it reaches its maximum value in the trans ($\delta$ = 180$^{\circ}$ ) conformation, its minimum in the totally eclipsed one ($\delta$ = 0$^{\circ}$ ), and intermediate values in the gauche conformers ($\delta$ = $\pm$60$^{\circ}$ ). Notwithstanding is undoubtable utility in rationalizing the origin of the three butane local minima, this RIC can be however neglected in the set defining the FF, as the torsional potential can be easily described by the combination of periodic functions only dependent on the dihedral.

A different situation arises for a slightly larger molecule, the PMME-H, shown in Figure 6. One of the lowest energy conformers is characterized by an intramolecular hydrogen bond, evidenced in Figure 6 with a dotted line, between the H atom of the carboxyl group and the Oxygen of the neighboring carboxylate. As both of these groups can easily change their relative orientation by varying (at least) either $\delta$ and $\chi$ dihedrals, the internal O-H distance depends on these soft ICs in rather complex fashion. In such cases, despite not necessary, it is convenient to include intramolecular distances in the RIC set defining the FF.

Figure 6: Some soft IC characterizing the PMME-H molecule.